مرحبا ، قبل أن نتحدث عن الخوارزميات و ماذا تعني الخوارزمية، ما رأيك أن نلعب لعبة. اللعبة التالية هي لعبة لي تخمين رقم عشوائي بين 1 و 21 ، في كل تخمين سوف اخبرك اذا كان تخمينك اكبر او اصغر من التخمين الصحيح. هل يمكنك تخمين الرقم الصحيح في اقل من 5 محاولات ؟

هل استغرق إيجاد الرقم الصحيح منك أكثر من 5 محاولات ؟ لا بد انك قمت بتخمين 1 ثم 2 ثم 3 و هكذا او قد خمنت بشكل عشوائي. دعني أخبرك بأنه باستخدام خوارزمية مثل خوارزمية البحث الثنائي لن تحتاج إلى أكثر من 5 محاولات لي تخمين الرقم مهما كان موضع الرقم الصحيح في تلك القائمة.

معنى كلمة خوارزمية في الحاسوب هي اتباع خطوات محددة لحل مشكلة ما. سميت الخوارزمية بهذا الاسم على اسم عالم الرياضيات المسلم محمد بن موسى الخوارزمي الذي عاش في القرن التاسع الميلادي، و ساهمت أعماله في تطوير الرياضيات بشكل كبير، اوضح الخوارزمي في كتبه كيف يمكن حل المشاكل الرياضية المعقدة بتجزئتها إلى أجزاء صغيرة بسيطة ثم حلها، وهذا تماما ما تفعله خوارزميات الحاسوب اليوم.

خوارزمية البحث الثنائي - Binary Search

أكثر الاستخدامات شيوعا لخوارزمية البحث الثنائي هي لي إيجاد عنصر محدد داخل قائمة مرتبة. كيفية عمل خوارزمية البحث الثنائي هي أنها تبدأ البحث من منتصف القائمة ثم يتم إقصاء نصف القائمة الذي لا يحتمل أن تكون عليه كلمة البحث ثم البدء من منتصف القائمة الذي بحتمل أن تكون عليه كلمة البحث، و يتم تضييق نطاق البحث هكذا بتكرار هذه الخطوات حتى يتم إيجاد كلمة البحث .

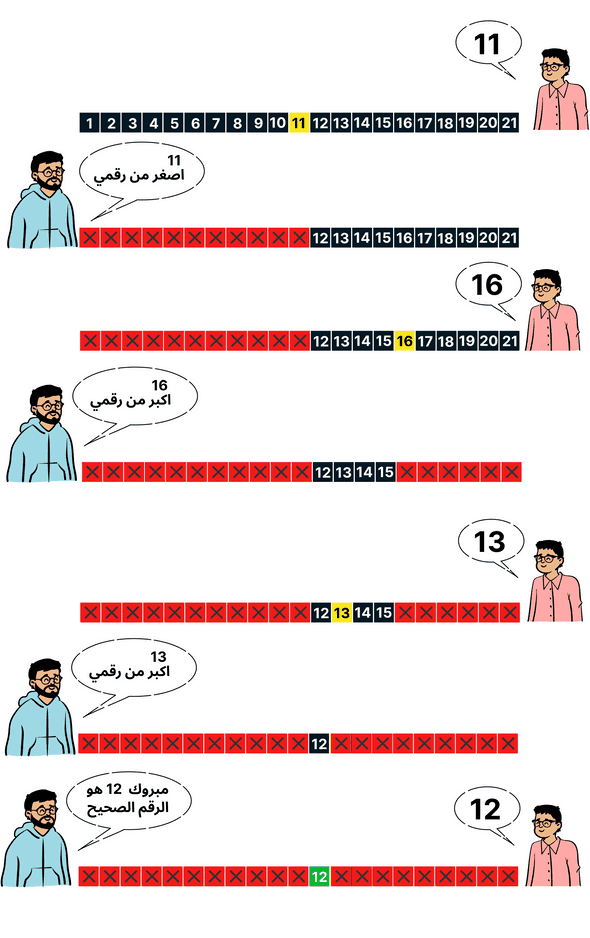
كمثال لعبة التخمين السابقة تتكون من قائمة ارقام مرتبة من 1 إلى 21، باستخدام خوارزمية البحث الثنائي فسوف تبدأ التخمين من المنتصف أي من الرقم 11، فإذا قلت لك أن 11 أصغر من التخمين الصحيح فهذا يعني أن الأرقام بين 11 و 1 لا يحتوي على التخمين الصحيح إذا سوف نقوم بإقصائه، ثم تبدأ مجددا البحث من منتصف الجزء الاخر يعنى الأرقام بين 11 و21 مثلا لنبدأ بالرقم 16 فإذا قلت لك أن 16 اكبر من التخمين الصحيح فهذا يعني إقصاء الأرقام من 16 إلى 21 و هذا يعني أن التخمين الصحيح يوجد بين الرقم 11 و 16 فإذا قمت بتخمين 13 و قلت لك أن 13 اكبر من التخمين الصحيح فهذا يعني أن التخمين الصحيح هو 12.

مبروووووك لقد تعلمت كيف تعمل خوارزمية البحث الثنائي، الآن بعد أن عرفت كيف تعمل خوارزمية البحث الثنائي هل يمكنك تخمين الرقم الصحيح في اقل من 6 محاولات.

كتابة الخورمية باستخدام جافاسكربت

خورزمية البحث الثنائي هي خورزمية مدخلاتها قائمة مرتبة من العناصر (يجب أن تكون قائمة مرتبة) و اذا كان كلمة البحث موجودة في القائمة, ترجع الخورزمية موضع ذلك العنصر في القائمة او المصفوفة و اذا كانت غير موجودة ترجع null .

قبل كتابة خوارزمية حاسوبية نحتاج أن نفهم الخوارزمية بتفاصيلها، ما هي مدخلات المشكلة ؟ و ما هي المخرجات؟ ما هي المتغيرات التي قد يحتاجها الخوارزمية، كمثال في اللعبة السابقة المدخلات هي قائمة الأرقام من 1 الي 42 و المخرجات سوف يكون التخمين الصحيح ، و ايضا نحتاج الى متغيرات لتتبع بداية و نهاية القائمة . يمكننا أن نصف الخوارزمية بهذا الشكل:

1. بداية القائمة = 0 ، نهاية القائمة = طول القائمة
2. وسط القائمة يجب أن يكون رقم صحيح
3. اذا كان الوسط يساوي ما نبحث عنه توقف. تم إيجاد الهدف
4. إذا كان التخمين اصغر من الهدف غير قيمة بداية القائمة الي موضع التخمين + 1
5. اذا كان التخمين اكبر من الهدف غير قيمة نهاية القائمة الي موضع التخمين - 1
6. ارجع للخطوة رقم 2

بالاعتماد على ذلك يمكننا كتابة الخورزمية باي لغة برمجة تفضلها. لكن الآن سوف نكتبها باستخدام لغة جافاسكربت .

const BinarySearch = (arr, target) => {
    // هذا السطر يحدد بداية المصفوفة او القائمة
    let startOfArray = 0

    // هذا السطر يحدد نهاية المصفوفة او القائمة
    let endOfArray = arr.length - 1
    
    // هذا السطر يكرر الكود ادناه الي ان يتم ايجاد الهدف
    while (startOfArray <= endOfArray) {

        //هذ السطر يحدد منتصف المصفوفة او القائمة
        let middleOfArray = Math.floor((startOfArray + endOfArray) / 2)

        // هنا يبدا التخمين من منتصف المصفوفة
        let guess = arr[middleOfArray]

        // اذا كان التخمين = الهدف يتوقف الكود هنا و يظهر موقع الهدف
        if (guess === target) return middleOfArray

        // اذا كان التخمين اكبر من الهدف
        // اجعل نهاية المصفوفة يساوي منتصف المصفوفة يعني مكان التخمين السابق
        if (guess > target) endOfArray = middleOfArray - 1

        // اذا كان التخمين اصغر من الهدف
        // اجعل بداية المصفوفة يساوي منتصف المصفوفة يعني مكان التخمين السابق
        else startOfArray = middleOfArray + 1
    }

    // في حال كان القائمة او المصفوفة لا يحتوى على
    // الهدف يتم اظاهر السطر في الاسفل
    return 'The target doesn’t exist in the array'
}

// خلينا نختبر الخورزمية
// الخورزمية اذا لقت الهدف هترجع مكان الهدف المصفوفة
// 0 في جافاسكربت ترتيب المصفوفة او القائمة يبدا من
let numbers = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
let names =["احمد", "بشير", "جميلة", "محمد"];

BinarySearch(numbers, 1) //  0
BinarySearch(numbers, 6) //  5
BinarySearch(numbers, 10) // 9

BinarySearch(names, 'محمد') // 3
BinarySearch(names, 'بشير') // 2
BinarySearch(names, 'احمد') // 0

وقت تشغيل الخوارزمية - algorithm runtime

algorithm runtime تعني الوقت الذي تحتاجها الخوارزمية لكي تعمل , في حالتنا في اللعبة السابقة عند تخمين الرقم بطريقة البحث العادية أي البدء ب 1، 2، 3، 4 وهكذا فإنه في أسوأ الحالات إذا كان الرقم الصحيح هو 42 فسوف نحتاج إلى 42 محاولة، لكن ماذا لو كانت القائمة تحتوي على أكثر من 42 رقم ، 7 مليون رقم مثلا فسوف نحتاج الى 7 مليون تخمين لإيجاد الرقم الصحيح.

الوضع مختلف مع خوارزمية البحث الثنائي مثلا في اللعبة تتكون من قائمة من 42 رقم ، باستخدام خوارزمية البحث الثنائي ستحتاج 6 تخمينات ، و إذا كانت القائمة تتكون من ٧ مليون رقم مثلا فسوف تحتاج إلى 23 تخمين فقط . خوارزمية قوية أليس كذلك!.

، بعض المصادر التى اعتمدت عليها في كتابة المقال و يمكنك الاطلاع عليها للتوسع اكثر في الموضوع الخوارزميات كتاب Grokking Algorithms و دروس على khan academy .